まずは極限等級がどのようにして導出されたのかを復習してみよう。 基本になっているのは、
『十分に暗い空の下で、平均的な人の瞳孔は7mmまで開き、肉眼では6等級の星まで見える』という経験則だ。瞳孔径が7mmなので、口径 D [mm] の望遠鏡を通すと、星は (D/7)2 倍の明るさに見える。 100倍の明るさで5等級変わるから、(5/2)*log (D/7)2 = 5*log(D/7) 等だけ明るく見えることになり、
LM = 6+5*log(D/7)の等級の星は、望遠鏡を通すと肉眼で見た6等星と同じ明るさになる。 これが極限等級 (LM) と言われている式だ。 しかし、これは限界等級ではない。上で述べたように、限界は背景の空の明るさにも依存している。 では、望遠鏡を通した空の明るさはどうなるだろうか? 星は十分に遠方にあるので、倍率を上げても点像のままだ。これを点光源と言う。 一方、空のように面積があるものは、倍率を上げると見掛けの大きさが大きくなるので暗くなってしまう。 これを面積体と呼ぶ。 面積体全体の明るさは、望遠鏡を通すと点光源と同様に (D/7)2 倍に明るくなるが、 望遠鏡の倍率を m とすると、見掛けの大きさが m 倍になることで単位面積当たりの輝度は (1/m)2 倍になってしまう。 つまり、面積体の単位面積当たりの輝度は (D/m/7)2 倍に見えることになる。 ここに現れた D/m が望遠鏡の出口の瞳の直径、射出瞳径だ (以下、略して瞳径とする)。
瞳径 = D/mD/m が瞳孔と同じ7mmになるときの倍率を望遠鏡の有効最低倍率と呼ぶ。 有効最低倍率では (D/m/7)2 = 1 なので、背景の空の明るさは肉眼で見たときと同じだ。 さて、この有効最低倍率で星を見ると、肉眼のときと同じ明るさの空の中に、LM 等級の星が6等星の明るさで見えるのだから、 上記の経験則に従えば、『この倍率のままでは』これより暗い星は見えないことになる。 これが極限等級の考え方だ。つまり、極限等級を正確に記述すると
『望遠鏡の有効最低倍率で見ることのできる最も暗い星の等級』なのである (実はまだ正しくないのだが、それについては両眼視と極限等級を参照)。
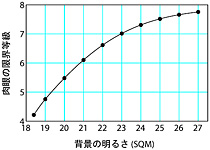
では倍率を上げるとどうなるか? 星は点光源なので明るさは変わらないが、背景の空は面積体なので暗くなり、もっと暗い星まで見えるようになる。 しかし、上記の経験則から外れた状況なので、そこから演繹して求めることはできない。 人がどこまで検出・識別できるのかという生理学の問題であり、物理学の問題ではないのだ。 しかし、 B. Schaefer による面白い論文 がある[1]。論文題目はずばり「望遠鏡の極限等級」。 生理学の実験によって得られた式を元に、様々な要因を考慮した限界等級の理論式を作り、それを実験で確かめたところ良い一致を見たという論文だ。 実に様々な要因が考慮されているが、肉眼の限界等級と背景の明るさの関係だけを抜き出すと
7.93 - 5*log(1+104.32-SQM/5)
 |
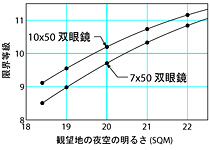
さて、背景の空は面積体なので、望遠鏡を通した背景の明るさは
SQM-5*log(D/m/7)になる。瞳径が D/m=1 [mm] の時には、約4等も背景が暗くなるのだ。 つまり、観望地の空が SQM=20 でも、瞳径が1mmの望遠鏡を通して見た空は SQM=24 に相当する暗さなのだ。 これから単純に望遠鏡の限界等級を出すと
限界等級 = 7.93 + 5*log(D/7) - 5*log(1+(D/m/7)*104.32-SQM/5)となる。論文では更に様々な要因を論じ補正を加えている。 例えば、個人的に面白いと思った補正には
- 夜空と星の色温度による補正。夜空は青系に寄っていて色温度が高い。
- 瞳径が大きいとき、眼球の周辺を通る光線の寄与は(減光により?)少なくなる。
 |
 |
 |
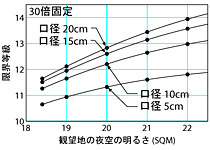
では、口径が違うもの同士を比べたらどうなるだろうか? 右図中は、口径20cm, 15cm, 10cm, 5cmの限界等級を倍率を30倍に固定してプロットしたものだ。 4等星程度しか見えない空 (SQM=18.4) では、口径をあげても限界等級はなかなか上がらないのが分かる。 口径の威力を発揮させるには、暗い空の下に行くか、倍率を上げる必要がある。 これは経験的に良く知られていることだ。
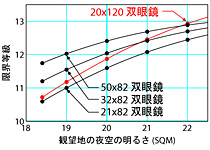
口径も倍率も違うもの同士を比べたらどうなるだろうか? 右図下は口径120mmで20倍固定の双眼鏡 (赤線) と、口径は82mmだが21倍、32倍、50倍に倍率が変えられる双眼鏡 (黒線) の限界等級を比べたものだ。 意外なことに、口径82mmでも倍率を上げることで20x120双眼鏡に肉薄していく様子が良く分かる。 SQM=18.4の空では、32倍で既に口径差を逆転しており、20x120より約0.5も暗い星まで見える。 SQM=21の暗い空でも、32倍で20x120と同じ限界等級であり、50倍まで上げると口径差を逆転することになる。 SQM=22の最高級の空でさえ、50倍まで上げれば、限界等級に関する限り20x120に迫るのだ。 意外な結果であるが、もし上で述べた背景の明るさと肉眼の限界等級の関係を信じるのであれば、この結果はそこからの単純な物理的帰結なので受け入れざるを得ない (マイナーな補正は無視しているが) 。
では、倍率を上げればどんどん暗い星が見えるようになるのかというと、もちろんそんなことはない。 あくまでも星が点光源として振舞う範囲内での話である。 星でも倍率を上げると回折像が見えるようになる。 回折像の大きさによって望遠鏡の分解能が決まるが、等光二重星の観測から得られたドーズの分解能は
分解能 = 115.8"/Dである (1"=1/3600度)。 一方、人の目の解像度は、視力1.0で60"=1'であり、楽に見分けるには2'の角度を要すると言われている (解像度を角度の分で表し、逆数をとったものが視力)。 望遠鏡の分解能まで (楽に) 解像するのに必要な倍率は有効倍率と呼ばれ[2]、それは
有効倍率 = 120"/(115.8"/D) ≒ Dとなる。これは瞳径が1mmとなる倍率である。 つまり、この倍率以上になると星の回折像が見えることになるが、回折像には大きさがあるので面積体として振舞い、Schaeferの関係式は成り立たなくなる。 しかし、Schaeferの論文には面白い記述がある。 限界等級に近い暗い星が、どの程度の大きさに広がったら点光源でなくなるかというと、900"=15'からだと言うのだ。 限界等級に近い二重星では、この角度以下を分解できないことを根拠として挙げている。 15'というと満月の1/2の大きさなので、少し大きすぎるのではないかという気もする。 しかし、吉田正太郎先生の本[2]には、暗い物体で楽に分解できるのは4'との記述もあり、 少なくとも有効倍率の2倍 (瞳径が0.5mm) 程度までは、Schaeferの関係式を使っても良さそうだ。 もちろん、光学系の収差や気流の乱れ等による星像の肥大化が起こらないことが条件だ。 これらによる星像の肥大化があれば、もっと低倍率でもSchaeferの関係式は成り立たなくなる。 短焦点アクロマートのように低倍率でも収差が残っているような光学系は限界等級に関して不利になる。
以上の話は、あくまでも限界等級に限った話である。 星雲や銀河などの面積体に対しては適用できない。 これらの天体は、倍率を上げると単位面積当たりの輝度が背景と同じように暗くなっていくので、背景とのコントラストは変化しない。 このような場合にどう見えるかは、やはり生理学のデータがないと分からない。 ただ、面積体に対する倍率効果は、限界等級のように口径差を逆転するほど大きなものではないように思える。 しかし、『限界等級は高いのに星雲が全く見えてこない』という状況にも違和感があるので、それなりの倍率効果はあるとも思える。 82mm対空双眼鏡の50倍で網状星雲を見たりすると、非常に暗くしか見えないのではあるが、小口径にしては意外と立派に(?)見えることに驚いたりもする。 星雲や銀河などの淡い天体に対しても高倍率性能は意外と重要で、高倍率性能がきちんとした小口径光学系は意外と侮れないものだ。
『望遠鏡の限界等級は倍率に関係なく口径で決まる』という誤解が広く蔓延しているように思えるが、倍率も口径と同じぐらい大切な要素なのだ。 もっとも、望遠鏡や双眼鏡の能力は限界等級だけではない。 そもそも星空を見て鑑賞するのが目的なので、迫力という要素は何より重要だ。 そして、迫力にはやはり明るさ、圧倒的な光量、すなわち口径が欠かせないものであることは承知している。
Schaeferの論文が提出されたのは1990年と比較的最近のことであり、どうやら眼視の能力についてはまだまだ多くの事柄が未解決のまま残されているようだ。 眼視は奥が深い。
【参考文献】