1. 明るさ
まず、双眼装置を通して見ると明るさはどう感じるのだろうか? これは生理学上の問題なので物理的に計算することはできないが、自分で簡単に実験することができる。 両目を開いたまま片目の視野の半分を黒い紙で覆ってみれば良い。 片目が紙で遮られている部分の景色は若干暗くなっているのが分かる。 光量を1/2倍にするNDフィルターを通した明るさと比べてみると、暗くなるとは言っても1/2倍にはなっていないのも分かる。 また、人の目で10%程度の光量の違いを (サイドバイサイドでなしに) 判別するのは難しいと言われていることを考えると、0.5倍以上0.9倍以下の明るさになっており、大雑把に0.7倍程度といったところだろう。 逆に言うと、
『人は両目を使って見ると、片目のときと比べ 1/0.7≒1.4倍の明るさに感じる』ということになる。 両目を使っても2倍にはならないところがポイントである。
ところで、この類の文献を読んでみると、√2≒1.4という数値が魔法数の様にあちこちに現れるが、どうやら両眼視の二乗和則 (quadratic summation rule) というのが元になっているようだ[1,2]。 二乗和則とは、右目と左目の感受性をそれぞれ CR, CL とすると、両目の感受性 C は
C = √(CR2+CL2)になるという経験則だ[1,2]。 右目と左目が同じ感受性であれば (CR=CL)、両眼視の感受性は単眼視に比べ √2 倍になることになる。 これは元々コントラストの感受性に関する実験から得られた関係式であるが、コントラスト以外にも色々と拡大解釈されているようだ。 二乗和則を単純に拡大解釈するというのは、『感受性 (sensitivity)』の定義が曖昧になるので (元々のコントラスト感受性はきちんと定義されている)、どう解釈すれば良いのか物理屋には理解し難い。 例えば、人の明るさに対する感受性は対数的でありダイナミックレンジが比較的広いことは有名な話だが、明るさそのものに二乗和則を適用するのと、明るさの対数に二乗和則を適用するのでは結果が異なってしまうからだ。 まぁしかし、結果的に明るさの感じ方に対しても単純に二乗和則が適用でき、両眼視では単眼視に比べ√2倍の明るさに感じるということになるようだ。
さて、望遠鏡に双眼装置を付けた両眼視では、片目に入る光量は元の1/2倍になっているので、 結局のところ (1/2)*1.4=0.7 より、
『双眼装置を使った両眼視では、双眼装置を使わない単眼視に比べ0.7倍の明るさに感じる』という結論に達する。 残念ながら、双眼装置を使うと、光学系による光のロスが全くなかったとしても、単眼視より暗く感じるのだ。
2. 極限等級
双眼装置を使うと単眼視よりも暗く感じるのだから、極限等級に関しても不利になると結論付けるのは早計である。 もう一度、根本から考えてみよう。 極限等級とは、『望遠鏡の有効最低倍率で見ることのできる最も暗い星の等級』であると極限等級の話で述べたが、実はまだ正しくない。 何故なら、ベースになっている「肉眼で6等星まで見える」という経験則は両眼視のときのものであり、これを単眼視の望遠鏡に当てはめて良いという根拠がないからである (むしろ良くないと考えるのが普通である)。 すなわち、両眼視をベースに導き出されたのだから、極限等級は本来
『双眼鏡の有効最低倍率で見ることのできる最も暗い星の等級』と記述すべきなのである。
では、両眼視と単眼視で限界等級はどのくらい違うのだろうか? これはSchaefer の論文でも考察されており、両眼視では星の明るさも背景の空の明るさも共に √2倍にする効果があるとしている[3]。 はじめこれを読んだとき、両眼視では上述のように約1.4倍に明るく感じることを根拠にしているのかと思ったが、そうではなかった。 根拠にしているのは、Pirenneによる生理学の実験[4]で、暗視環境下で点光源の点滅の何割が検出できるかを両眼視と単眼視で比べた実験だ。 実験の結果は、両目それぞれが独立な検出器として振る舞い、ノイズの中から点光源を検出するという確率モデルで良く説明できるとのことだ[4]。 ノイズの起源としてPirenneは、物理的なもの (量子論的なものなど) と生物的なものを挙げているが、いずれにせよ目を閉じたり暗がりを見たりすると我々の視野には確かにノイズが乗っているのが分かる。 さて、Pirenneの論文には√2という値はどこにも書かれていないが (よってSchaeferが何を根拠に√2倍と考察しているのか不明であるが)、両目が独立な検出器として振舞い、ノイズが白色ノイズであると仮定すると、2つを合成したノイズレベル (雑音量の分散) は1/√2倍になり、SN比が√2倍になるというのは工学の基礎である。 すなわち、信号の検出限界が √2倍だけ向上することを意味しており、結局、両眼視は単眼視と比べて
(5/2)log(√2) ≒ 0.38等だけ限界等級が上がることを意味している。 これは、星の明るさも背景の明るさも√2倍にするというSchaeferの考察 (結果として限界等級はあまり上がらない) とは異なるものであるが、個人的にはSchaeferの考察には同意できない。 Pirenneの結論を素直に適用するなら、限界等級を0.38等上げるべきである。 文献[5]も、実際の両眼視による限界等級の向上がSchaeferの結果よりも大きいことから、同様の事を指摘している。
また、文献[6]では13インチの巨大双眼望遠鏡と16インチのドブソニアン望遠鏡の限界等級を実際に比較しており、双眼望遠鏡の限界等級は1.4倍〜1.5倍の口径の望遠鏡の単眼視と同等であるという実験結果を得ている。 これは、両眼視が単眼視に比べ
5log(1.4) ≒ 0.7等も限界等級が上がるという (少々驚くべき) 実験結果である (ちなみに上記の0.38等というのは、双眼望遠鏡の限界等級が√√2≒1.2倍の口径の望遠鏡の単眼視と同等であることに対応する)。 文献[7]では、さまざまな双眼鏡をフィールドテストした結果が報告されており、Schaeferの関係式との比較も行われている。 そこでは、両眼視と単眼視の限界等級の差は0.2等だと報告されている。 このように、両眼視での限界等級の向上については諸説あるようであり、また個人差も大きいように思えるが、まとめると、
『両眼視は単眼視に比べ、0.2〜0.7等だけ限界等級が上がる』との結論に達する。 以下では主に 0.38等という値を使うことにする。
さて、これらをSchaeferの限界等級の式に当てはめてみよう。 Schaeferの式も肉眼 (両眼視) での実験結果がベースになっているので、双眼鏡の限界等級を表している。 よって、口径 D [mm]、倍率 m の望遠鏡の単眼視では、Schaeferの式より 0.38等だけ限界等級が下がることになる。
単眼視の限界等級 = 7.93 + 5*log(D/7) - 5*log(1+(D/m/7)*104.32-SQM/5) - 0.38双眼装置を使った場合、片目に入る光量は半分になるので口径は双眼鏡換算で D/√2 になるが、両目で星を検出するので0.38の補正は不要となる。
双眼装置の限界等級 = 7.93 + 5*log(D/√2/7) - 5*log(1+(D/√2/m/7)*104.32-SQM/5)これらを条件を色々と変えて比べてみよう。
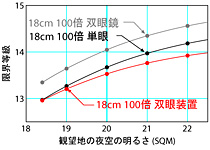 |
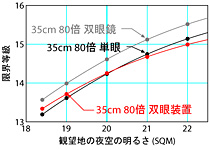 |
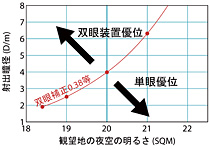 |
右図中は、口径35cmの望遠鏡の場合についてプロットしたものだ。 ドブソニアン式のF値の小さい望遠鏡を想定し、倍率は口径にしては低めの80倍に設定している。 単眼視と双眼装置の限界等級が、SQM=20 を堺にして逆転してしまっているのが分かる。 意外なことに、SQM=18.4のように明るい空では、双眼装置を使った方が僅かではあるが限界等級は高いのである。 また、逆転現象が起こるくらいなので、総じて単眼視と双眼装置の差は小さいことが分かる。 大変に意外な結論であるが、あくまでも両眼視が単眼視より0.38等だけ限界等級が上がると仮定した場合の結果である。
ところで、この逆転現象はいつ起こるのだろうか? それを決めているのは望遠鏡の射出瞳径 (D/m) である。 右図下は、単眼視と双眼装置の限界等級が等しくなる瞳径を、観望地の空の明るさ (SQM) の関数としてプロットしたものだ。 この曲線より左上側では双眼装置を使った方が限界等級は高く、逆に右下側では単眼視の方が高くなる。 逆転現象が起きる理由は、極限等級の話で述べたように、瞳径が比較的大きい領域で倍率を固定した場合、空が明るいと限界等級は口径にあまり依存しなくなるからである。 このような状況では、口径を1/√2倍に落としてでも、両眼視による検出能力の向上を活用した方が有利に働くことになる。
以上の話は、双眼装置による光量ロスや像劣化がない理想的な状況での話であり、また、あくまでも点光源である星の限界等級に限った話である。 もちろん、星雲や銀河などの面積体に対しても、両眼視による検出能力の向上はあると思われるが、面積体に対しては単眼視の倍率効果でさえ良く分かっていない状況だ。
【参考文献】
- F. W. Campbell and D. G. Green, "Moocular versus binocular visual acuity", Nature 208, 191 (1965).
- G. E. Legge, "Binocular contrast summation --- II. Quadratic summation", Vision Res. 24, 385 (1984).
- B. Schaefer, "Telescopic limiting magnitudes", publication of the astronomical society of the pacific 102, 212 (1990)
- M. H. Pirenne, "Binocular and uniocular threshold of vision", Nature 152, 698 (1943).
-
N. O. Carlin, "About Bradley E. Schaefer: Telescopic limiting Magnitudes".
- A. Otte, "The binocular summation factor and its relevance for deepsky observing" Part 2, Measurements to determine the value of the factor.
- Ed Zarenski, "Limiting Magnitude in Binoculars".