ところで、RFTを視野内の星の数を最大化するものとすると、その条件はアイピースの見掛視界に大きく依存することになる。 それだと話が複雑になりすぎるので、ここでは主に視野内の星密度を最大化することを考えることにする。
まず簡単にRFTの歴史を振り返って見よう[1]。 1936年、S. L. Walkden は『小口径でも大口径望遠鏡をしのぐ事がある』として RFT の概念を提唱した[2]。 その論文には、簡易的な星の等級分布を使うと、口径2.5インチ (約6cm)、8.4倍という小口径望遠鏡で視野内の星密度が最大になること、 またもう少し正確な星の等級分布を使うと、口径7インチ (約18cm)、24倍の望遠鏡で最大になることが示されている[2]。 その後の1980年、G. Shaw は Sky and Telescope誌で、最新の星の等級分布を使うと口径9インチ (約23cm) で最大になることを示しているそうだ[1]。 ところが、1996年に H. R. Suiter は、星の等級分布によって最適な口径は1.5インチ (約4cm) から12インチ (約30cm) まで変わってしまうことを指摘しているとのことだ[1]。 その為かどうか分からないが、RFTは広義には『広視野望遠鏡』のことであり、単純に低倍率・広実視界が得られる望遠鏡を意味することもある。 ところで、RFTの条件がこんなにも変わるとは、いったいどういうことだろうか? もう一度、はじめから考察してみることにしよう。
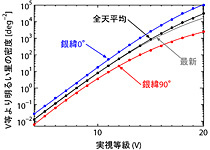 |
図1 |
Log10 N(V) = -0.0003 V3 + 0.0019 V2 + 0.484 V - 3.82であると書いてある (ただし 4≦V≦25 )。 この式の出典が不明なので良く分からないが、おそらくこれが最新モデルでの近似式なのだろう。 この式にV=10を代入すると N(10)=100.91 [/平方度] であり、全天は4π [平方ラジアン] ≒ 41,253 [平方度] なので、 全天で10等より明るい星の数は N(10)* 41,253 ≒ 約33,500個 ということになる。 しかし、星の密度は天の川の中と外では大きく異なる。 銀河座標は、天の川銀河の銀河面を緯度0度と定義した座標系であるが、文献[4]には全天平均に加え、銀緯毎の N(V) が表になっている。 銀緯0度の N(V) は天の川の中心線付近での平均星密度、銀緯90度の N(V) は天の川より最も離れたところでの平均星密度である。 この表の 4≦V における Log10 N(V) の値を V の3次多項式でフィットすると
全天平均: Log10 N(V) = -0.000280 V3 + 0.00275 V2 + 0.471 V - 3.80となった。 図1は、これら全天平均 (黒)、銀緯0度 (青)、銀緯90度 (赤) の N(V) をプロットしたものだ。 また、上記文献[3]の最新モデルによる全天平均を灰色でプロットしてあるが、文献[4]の全天平均と似たようなものだ。
銀緯 0度: Log10 N(V) = -0.000471 V3 + 0.0105 V2 + 0.393 V - 3.26
銀緯90度: Log10 N(V) = -0.000133 V3 - 0.00668 V2 + 0.575 V - 4.38
次に、夜空の明るさが SQM [等級/平方度] の観望地における口径D [mm]、倍率mの双眼鏡の限界等級は、極限等級の話で述べたSchaeferの関係式[5]により
V = 7.93 + 5*log(D/7) - 5*log(1+(D/m/7)*104.32-SQM/5)である。 以下、これを使って条件を探ることにする (望遠鏡の限界等級は両眼視と極限等級を参照)。 よって、ここで考えているのはRFTの条件ではなく、RFB (リッチェスト・フィールド双眼鏡) の条件ということになる。 RFTについては後で簡単に触れる。 倍率mの双眼鏡の視野内の星密度は
視野内の星密度 = N(V)/m2なので、これをSQM毎に口径Dと倍率mで最大化すれば良い。 ところで、
倍率mを固定したときの限界等級Vは、口径Dで単調増加する (倍率が同じなら口径が大きいほど限界等級は高い)。また、倍率mを固定したときの視野内の星密度はVで単調増加するので、結局、倍率mを固定したら口径Dは大きいほうが視野内の星密度は高くなる。 よって、視野内の星密度が最大になるのは必ず有効最低倍率のときで、すなわち瞳径が7mm (D/m=7) のときである。
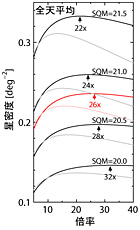 |
図2 |
 |
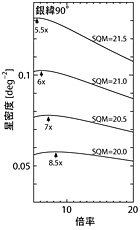 |
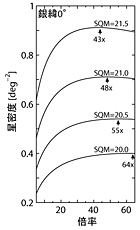
図3 |
図4 |
ところで、双眼鏡で星空を見たときに、「わぁ、星がいっぱいだ!」と歓声を上げたくなるのは、やはり天の川を見たときではないだろうか? そこで、天の川を見たときの星密度を最大化するRFBの条件を、もう少し探ってみよう。
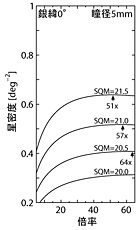 |
図5 |
7x50双眼鏡: 0.68xπ(50/2)2 ≒ 1,340個となり、10x50の方が多くなる。 実視界がほぼ同じなので、10x50の方が限界等級が高ぶんだけ視野内の星の数が多くなるからだ。
10x50双眼鏡: 0.50xπ(65/2)2 ≒ 1,660個
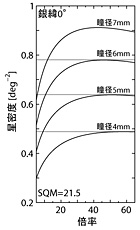 |
図6 |
以上を踏まえた上で、私の独断と偏見から、最大星密度0.91[/平方度]の8割にあたる約0.73[/平方度]以上の星密度が得られること (と準広角タイプであること) をRFBの条件として採用することにし、次の結論に達する。
RFBとは、6mm以上の大きな瞳径を持ち、なおかつ瞳径7mmなら9倍以上、瞳径6mmなら20倍以上の倍率があり、見掛視界が (旧表示で) 60度以上の双眼鏡である。ちなみに、高倍率側の境界は100倍 (口径60cm) を超えるところにあるので、現実的にあまり考えなくても良い。 このようにRFBを定義すると、市販のプリズム双眼鏡で該当するものは極めて限られていることが分かる。 RFBと言えるだけの大瞳径かつ広視野を実現するには大きなプリズムが必要になり、大型化・コスト高を招いてしまうので商品になり難いということだろう。 また、RFBをこのように定義すると、直ちに次の結論が得られる。
双眼装置を使ってRFBを作ることはできない。双眼装置は望遠鏡の1つの像を2つに分割するので、片目の光量は半分になってしまい、双眼鏡に換算したときの瞳径 (等価な明るさになるという意味での) は最大でも 7mm/√2 ≒ 5mm にしかならないからだ。
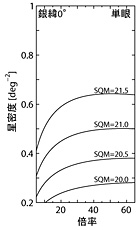 |
図7 |
そもそも、片目を瞑って見えなくなるような最微光星は「星がいっぱいだ!」という感じ方にはあまり寄与せず、もっとはっきり見える星の密度が重要だという考え方もあるだろう。 例えば、限界等級よりも0.38等以上明るい星だけの密度を考えることにすると、図7をそのまま (望遠鏡ではなく) 双眼鏡での結果だと考えれば良い。 この場合でも、ある程度倍率が高くなると、星密度は倍率を変えてもあまり変化せず、瞳径自体が重要なファクターになっている事に変わりはないので、RFBの条件も大きくは変わらない。 ただし、倍率は多少高倍率側にずれる (20%程度)。
極限等級の話では、口径が同じなら倍率を多少上げた方が (結果的に瞳径を小さくした方が) 限界等級は上がるし、星雲の見応えも増すという結論だったが、 星密度に関しては瞳径が大きい方の圧勝という全く逆の結果になってしまった。 こうして双眼鏡選びは混迷して行くのである。
追記 (2019/03)
改訂 (2021/03)
アイピースの見掛視界がどのように影響するのかを見るため、私が使っている機材で視野内の星数を計算してみた。 最高級の星空 (SQM=21.5) で天の川 (銀緯0度方向) を見たときに期待される視野内星数だ。 望遠鏡は等倍の双眼装置で使うものとし (よって口径は1/√2とする)、倍率可変の機材では星数が最大となるようなアイピースを選んだ。 また、収差や周辺減光は無視し視野周辺でも視野中心と同じように星が見えるものと仮定している。 なお、視野内星数は『N(V) x 実視界面積』なので、視野内星密度 N(V)/m2 から『N(V)/m2 x 見掛視界面積』を使って求める際の見掛視界は、旧表示の『実視界 x m』を使う必要がある。 結果は次の通り。
| 機種 | 倍率x口径 | 限界等級 V | 星密度 N(V)/m2 | 見掛視界 | 視野内星数 |
| 2x54 UWA | 2x14 | 7.9等 | 0.45/平方度 | 72度 | 約1,800個 |
| 8x30 EII | 8x30 | 10.1等 | 0.32/平方度 | 70度 | 約1,200個 |
| NL 10x32 | 10x32 | 10.4等 | 0.27/平方度 | 75度 | 約1,200個 |
| MHG 8x42 | 8x42 | 10.6等 | 0.50/平方度 | 66度 | 約1,700個 |
| 10x50 FMT-SX | 10x50 | 11.0等 | 0.50/平方度 | 65度 | 約1,700個 |
| WX 10x50 | 10x50 | 11.0等 | 0.50/平方度 | 90度 | 約3,200個 |
| WX + TCON-17X | 17x56 | 11.6等 | 0.32/平方度 | 90度 | 約2,000個 |
| HIGH LANDER | 21x82 | 12.3等 | 0.43/平方度 | 63度 | 約1,300個 |
| 20x120 III | 20x120 | 12.7等 | 0.73/平方度 | 60度 | 約2,100個 |
| mewlon-180B | 90x129 | 13.8等 | 0.11/平方度 | 64.5度 | 約400個 |
| NEBULITE 35cm | 68x254 | 14.8等 | 0.45/平方度 | 64.5度 | 約1,500個 |
1位は大差をつけて WX 10x50。 瞳径は5mmなので上記のRFBの条件を満たしていないのだが、90度という驚異的な見掛視界の広さが効いている。 2位は 20x120 III。 上記RFBの条件を唯一満たしている機種で、実際、視野内星密度は唯一抜きん出ている。 他は高倍率機の mewlon を除けば似たり寄ったりの星数だが、強いて順位付けすると 2x54 UWA が3位となる。 ただ、これだけの低倍率ともなると天の川で視野が満たされない (銀緯0度の星密度で代表できない) ので、もはやこの計算結果にあまり意味はない。 ちなみに、同じ機材で倍率を変えた場合にはなるが、1.7xテレコンを使って倍率を上げた WX 10x50 もランキングに加えると、星数2,000個で第3位となる。 瞳径は3.3mmしかないのにこの星数とは、超広視界の威力は凄いな。
あと私は使っていないが、気になる幾つかの機種についての計算結果を参考までに次に示す。
| 機種 | 倍率x口径 | 限界等級 V | 星密度 N(V)/m2 | 見掛視界 | 視野内星数 |
| SF 8x42 | 8x42 | 10.6等 | 0.50/平方度 | 67度 | 約1,800個 |
| NL 8x42 | 8x42 | 10.6等 | 0.50/平方度 | 72.8度 | 約2,100個 |
| MHG 10x42 | 10x42 | 10.8等 | 0.40/平方度 | 69度 | 約1,500個 |
| NL 12x42 | 12x42 | 10.9等 | 0.32/平方度 | 78度 | 約1,500個 |
| WX 7x50 | 7x49 | 10.6等 | 0.68/平方度 | 74.9度 | 約3,000個 |
| SLC 8x56 | 8x56 | 10.9等 | 0.71/平方度 | 60.8度 | 約2,100個 |
| 10x70 SP | 10x70 | 11.4等 | 0.75/平方度 | 51度 | 約1,500個 |
| 10x70 I型 | 10x70 | 11.4等 | 0.75/平方度 | 65度 | 約2,500個 |
| 18x70 IF | 18x70 | 11.9等 | 0.41/平方度 | 72度 | 約1,700個 |
| 15x110 PNB-1 | 15x105 | 12.2等 | 0.82/平方度 | 90度 | 約5,200個 |
| 25x120 | 25x120 | 12.9等 | 0.58/平方度 | 72.5度 | 約2,400個 |
| 25x150 MT-SX | 25x150 | 13.2等 | 0.75/平方度 | 67.5度 | 約2,700個 |
やはり大瞳径で視界を広くとった機種の威力は凄いな。 では、どこまで視野内星数を増やすことができるのだろうか? 瞳径7mm、超高視界100度の双眼望遠鏡の視野内星数は…
| 倍率x口径 | 限界等級 V | 星密度 N(V)/m2 | 見掛視界 | 視野内星数 |
| 30x210 | 13.8等 | 0.90/平方度 | 100度 | 約7,100個 |
| 20x140 | 12.9等 | 0.86/平方度 | 100度 | 約6,800個 |
| 15x105 | 12.3等 | 0.82/平方度 | 100度 | 約6,400個 |
| 10x70 | 11.4等 | 0.75/平方度 | 100度 | 約5,900個 |
視野内星数が約7,000個超!
私が生きている間に実現可能になるのだろうか?
追記 (2019/09)
ちなみに視野内星数 1,000個だの 2,000個だのとは、一体どの程度のものなのだろうか? 図6は星数に応じた視野をシミュレートしたものだ。 等級分布は全く適当で、単純に 2,000個、1,400個、1,000個の点を、大きさをランダムに変えながらプロットしただけのもの (微光星の方が多くなるように工夫はしているが)。 概ね雰囲気は出ているように思う。
 |
 |
 |
図6 星数 2,000個 |
星数 1,400個 |
星数 1,000個 |
追記 (2020/08)
倍率、口径(mm)、実視界(度)と夜空の明るさ(SQM)を入力し『計算』のボタンを押すだけで、限界等級、星密度と視野内星数が計算できるようにしてみた。 SQMは、肉眼で4.5等星ぐらいが見える都市郊外や地方都市でSQM=18.5、天の川が分かる空でSQM=20、肉眼で6等星まで見える遠征地でSQM=21、最高級の空でSQM=21.5ぐらいと言ったところだと思う。
【参考文献】
- Richest Field Telescopes by Mel Bartels.
- S. L. Walkden, "The richest-field telescope", Popular Astronomy 44, 146 (1936).
- How many stars are in the sky?
- C. W. Allen, Astrophysical Quantities, Third Edition (Atholone press, London, 1973), p. 244.
- B. Schaefer, "Telescopic limiting magnitudes", publication of the astronomical society of the pacific 102, 212 (1990).